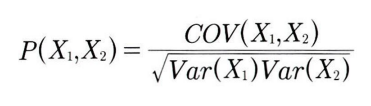Post

[ML기초세션]_1주차

Posted Updated
By JINGI CHAE
19 min read

ML모델의 성능에는 알고리즘의 우수성, 파라미터 최적화보다 데이터를 올바르게 파악하고 효과적으로 가공하는 것이 더 중요하다!

EDA(탐색적 데이터 분석)과 데이터 시각화는 구별해야 한다.

EDA: 시각화를 이용하지만 최종 목적은 분석 결과를 커뮤니케이션하기 위함이다.

1. EDA(Explanatory Data Anaylysis)

기술통계와 데이터 시각화를 통해 데이터의 특성을 파악하는 것. 극단적인 해석은 피해야 하며 지나친 추론이나 자의적 해석도 지양해야 함.

  • EDA의 주요 목적
    1. 데이터 형태와 척도가 분석에 알맞은지 확인
    2. 데이터의 평균, 분산, 분포, 패턴 등을 통해 데이터 특성 파악
    3. 데이터 결측치나 이상치 파악 및 보완
    4. 변수 간 관계성 파악
    5. 분석 목적과 방향성 점검 및 보정

엑셀을 활용하여 데이터 샘플을 뽑아서 직접 살펴볼 수 있다. +피벗 테이블, 간단한 그래프를 활용할 수도 있다.

2. 공분산과 상관성 분석

데이터 탐색 과정에서 평균, 분산 등을 통해 변수들의 특성을 파악한 뒤 변수간의 관계를 파악해야 한다. 타깃 변수 Y와 입력 변수 X와의 관계는 물론, X들 간의 관계도 살펴봐야 한다

이렇게 함으로써 독립 변수 변화에 따른 종속 변수의 변화량을 크게 하여 통계적 정확도를 감소시키는 다중공선성을 방지할 수 있다.

->변수 간의 상관관계를 파악하는 대표적인 개념: 공분산 & 상관계수

(상관 분석을 위해 데이터가 등간이나 비율 척도이고 두 변수가 선형적 관계라는 기본가정) 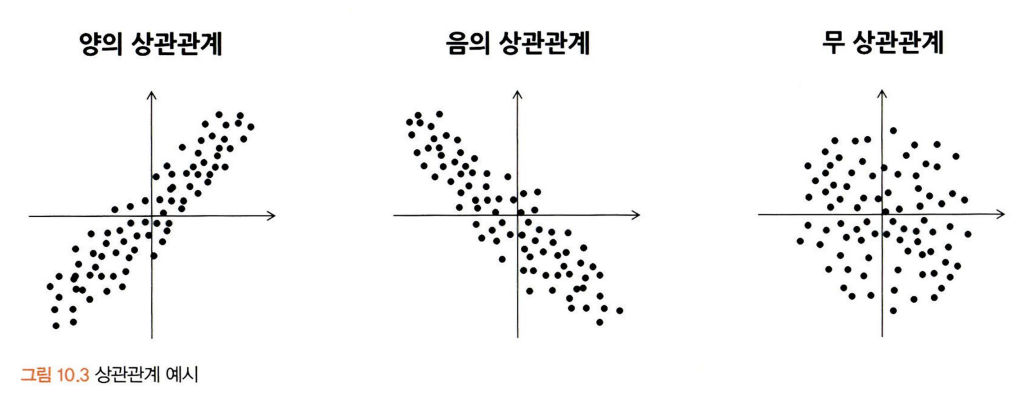'img1'

  • 공분산:
    1. 서로 공유하는 분산
    2. 분산은 한 변수의 각각의 데이터가 퍼진 정도를 나타내지만, 공분산은 두 분산의 관계를 나타낸다.

X 데이터셋에 X1, X2변수 존재 -> X1변수 값의 편차와 X2 변수 값의 편차를 곱한 값을 모두 더한 후 전체 개수 n(표본은 n-1)으로 나눈다. -> 두 변수의 공통적인 분산 정도 파악 가능

'img2'

  • 공분산 = 0 : ‘무 상관관계’, X1과 X2는 선형적인 관계가 없다.
  • 공분산 > 0 : ‘양의 상관관계’, X1이 커지면 X2도 커진다.
  • 공분산 < 0 : ‘음의 상관관계’, X1이 커지면 X2는 작아진다.
  • 공분산 = 1 or -1 : X1과 X2는 완벽한 직선관계다.

공분산은 단순한 원리로 변수 간 상관관계를 수치화한 것이기에 한계가 존재한다. 각 변수 간의 다른 척도 기준이 그대로 반영되어 공분산 값이 상관성 정도를 나타내지 못한다. -> 이를 해결하기 위해 피어슨 상관계수를 많이 사용

  • 상관계수:
    1. 변수 X1과 X2가 함께 변하는 정도(=공분산)를 X1과 X2가 변하는 전체 정도로 나눈 것.
    2. 함께 변하는 정도는 전체가 변하는 총량을 초과할 수 없기에 상관계수는 [-1, 1] 범위 안에 위치한다.

'img3'

'img4'

'img5'

  1. 기울기가 위로 향하면 양의 상관관계, 아래로 향하면 음의 상관관계
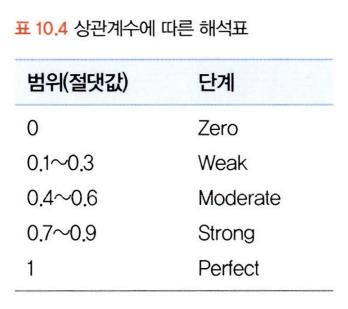
  2. 절댓값이 0.7 정도만 되어도 선형적 관계 나타남
  3. 절댓값이 0.3 이하가 되면 상관성을 인식하기 모호해짐

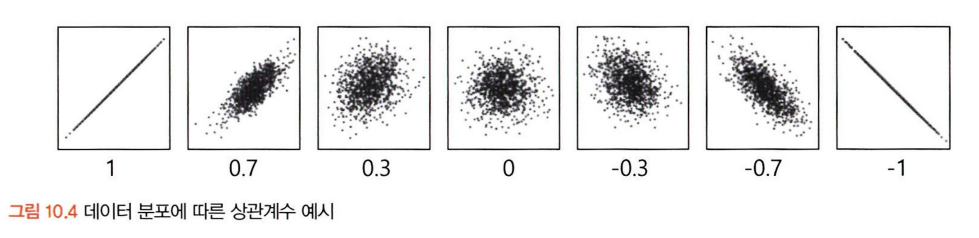
산점도의 기울기와 상관계수는 관련이 없다!!

  • 분산의 관계성이 같다면, 기울기에 무관하게 상관계수는 동일하다.
  • 상관계수가 높다는 것은 X1이 움직일 때 X2가 많이 움직인다는 뜻이 아니라, X2를 예상할 수 있는 정확도, 즉 설명력이 높다는 것이다.

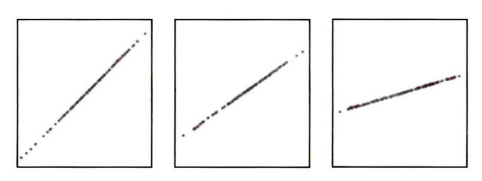'img' ex) 위의 사진에 나타난 3개의 그래프 모두 상관계수는 1로 동일하지만 그래프의 모양은 다르다.

상관분석은 두 변수의 선형관계만을 측정하기에 2차 함수와 비슷한 모양이 될 경우, 상관계수가 매우 낮게 측정될 수 있다.

1
2
3
4
5
6
7
8

# 공분산 확인
df.cov()

# 피어슨 상관계수 확인
df.corr()

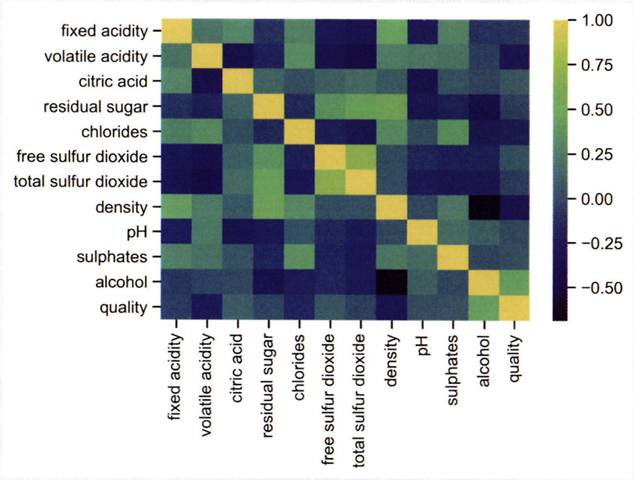
# 히트맵 시각화
sns.heatmap(df.corr(), cmap='viridis')

'img6'

노란색에 가까울 수록 양의 상관관계,

보라색에 가까울 수록 음의 상관관계

1
2
3
4
5
6

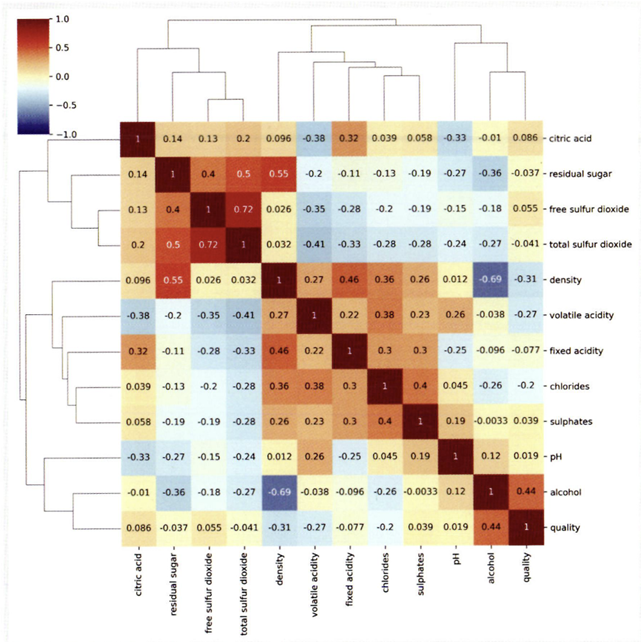
# clustermap 히트맵 시각화
sns.clustermap(df.corr(),
                annot = True, # 각 셀의 상관계수를 숫자로 표현
				cmap = 'RdYlBu_r', # 차트 색상
				vmin = -1, vmax = 1, # 색상 축의 최솟값 -1, 최댓값 1
				)

'img7'

3. 시간 시각화

시점 요소가 있는 데이터는 시계열 형태로 표현하여 시간의 흐름에 따른 데이터의 변화를 표현할 수 있다. 시간 시각화는 선그래프 형태의 연속형과 막대그래프 형태의 분절형으로 구분할 수 있다.

연속형 시각화

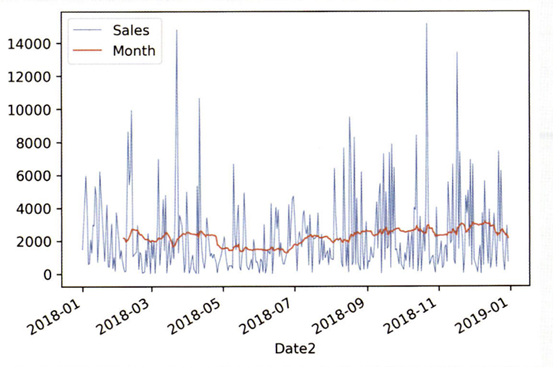
선그래프는 시간 간격의 밀도가 높을 때 사용한다.

데이터 양이 너무 많거나 변동이 심하면 데이터를 파악하는 것이 어렵기에 추세선을 넣어 데이터의 흐름을 안정된 선으로 표현할 수 있다.

추세선을 그리는 가장 일반적인 방법, 이동평균(Moving Average) 방법: 데이터의 연속적 그룹의 평균을 구하는 것.

1
2
3
4
5
6
7

# 30일 이동 평균 생성
# rolling(window=30) : 30일 간의 이동 윈도우를 나타냄
df_line['Month'] = df_line['Sales'].rolling(window = 30).mean()

# 선그래프 시각화
ax = df_line.plot(x='Date2', y='Sales', linewidth = "0.5")
df_line.plot(x='Date2', y='Month', color='#FF7F50', linewidth="1", ax=ax)

'img8'

분절형 시각화

  1. 막대그래프, 누적 막대그래프, 점 그래프 등으로 표현한다.
  2. 시간의 밀도가 낮은 경우에 활용하기 좋고 값들의 상대적 차이를 나타내는 것에 유리하다.
  3. 누적 막대그래프는 한 시점에 2개 이상의 세부 항목이 존재할 때 사용

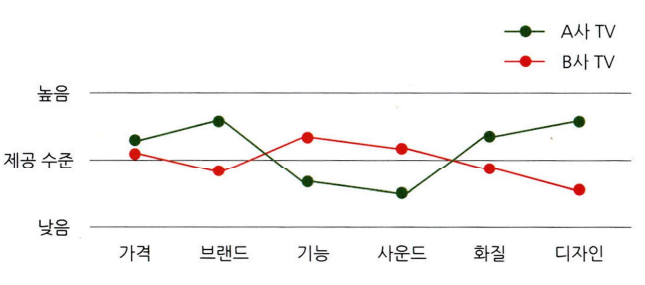
4. 비교 시각화

그룹별 차이를 나타내기 위한 비교 시각화는 (누적) 막대 그래프로도 가능하지만, 그룹별 요소가 많아지면 히트맵 차트를 이용하는 것이 효과적! 히트맵의 각 행은 그룹, 열은 요소에 해당됨

히트맵 차트를 다른 시각화 방법에 비해 그리는 것이 까다롭기 때문에, 현재 데이터의 구조와 자신이 확인하고자 하는 목적을 정확히 파악한 다음 차트를 그려야 한다.

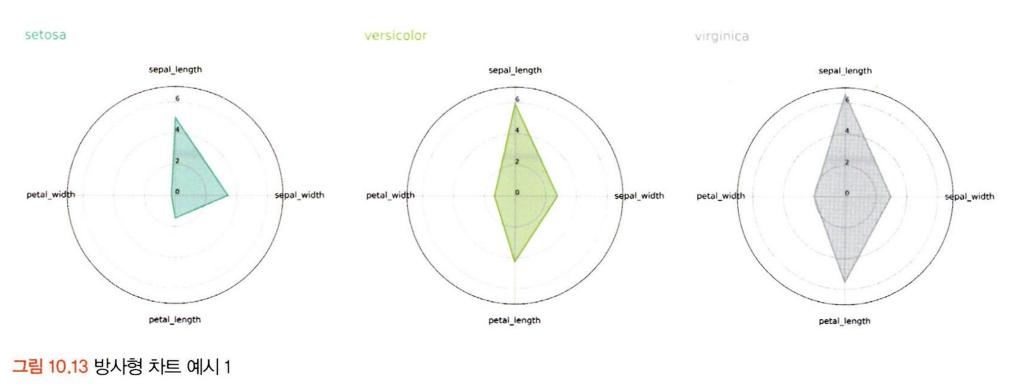
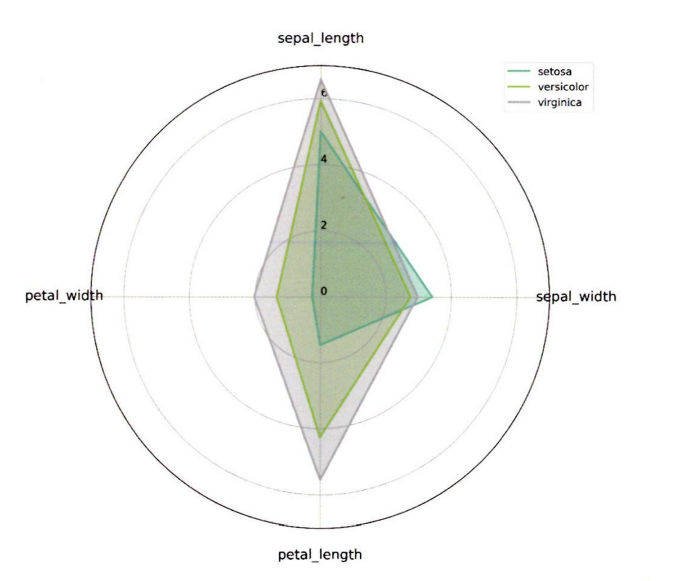
방사형 차트

  • 하나의 차트에 하나의 그룹 'img9'

  • 하나의 차트에 모든 그룹 'img10'

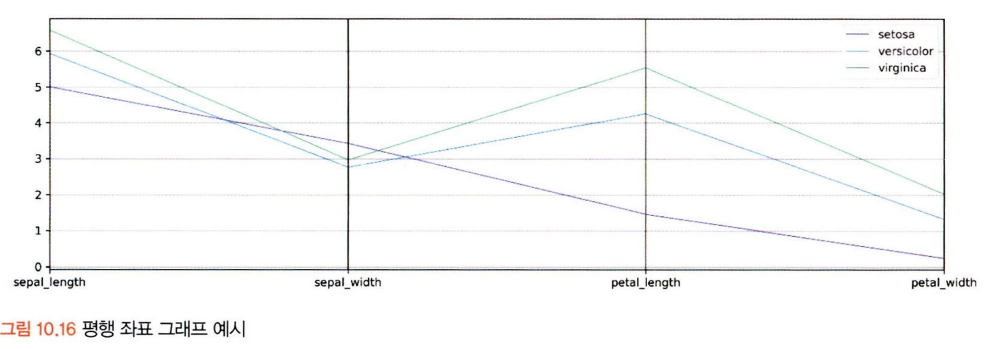
평행 좌표 그래프

평행 좌표 그래프를 보다 효과적으로 표현하려면 변수별 값을 정규화 하면 된다. 가장 낮은 값은 0%로, 가장 높은 값은 100%로 변환하여 차이를 드러낸다.

-> 여러 변수를 평행으로 배치하여 표현하기에 각 그룹의 요소별 차이 수준을 효과적으로 파악할 수 있고, 집단적 경향성을 표현함에 있어서 용이함.

'img11' 'img12'

5. 분포 시각화

매우 단순한 시각화 방법이지만 데이터를 파악함에 있어서 매우 중요한 분포 시각화! 데이터가 처음 주어졌을 때, 변수들이 어떤 요소로, 어떤 비율로 구성되어 있는지 확인하는 단계. 연속형과 같은 양적 척도인지, 명목형과 같은 질적 척도인지 구분해서 그린다.

양적 척도
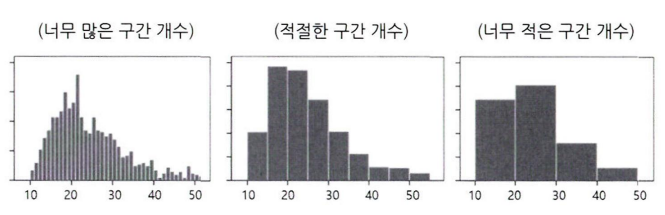
막대그래프, 선그래프, 히스토그램
  • 히스토그램:
    1. 겹치지 않는 변수의 구간을 동일하게 나눠서 구간별 도수를 막대그래프로 표현.
    2. 각 구간을 bin, 구간의 높이는 밀도(density)라고 한다. 이 밀도는 가로축 단위 구간에 속한 값의 비율을 나타냄 'img13'

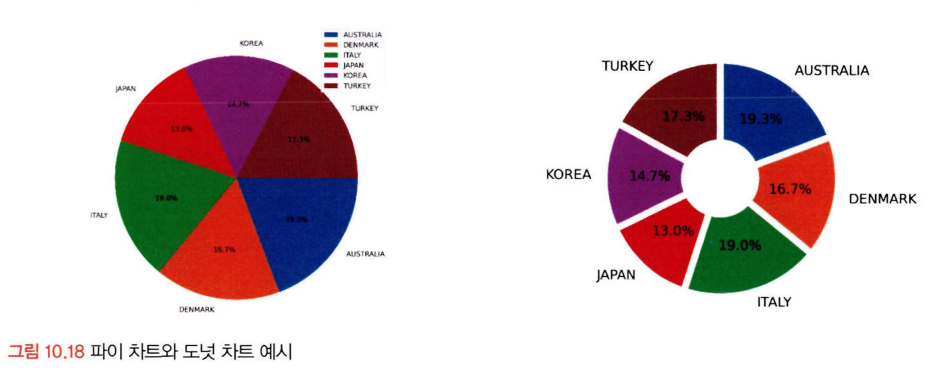
질적 척도

구성이 단순한 경우: 파이 차트, 도넛 차트 'img14'

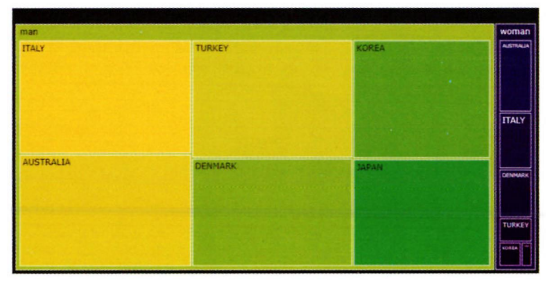
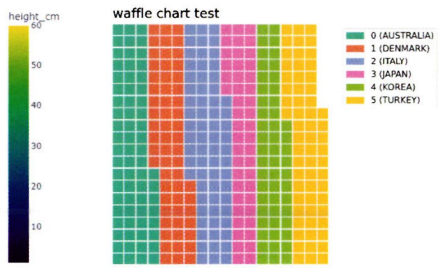
구성이 복잡한 경우: 트리맵 차트, 와플 차트

  • 트리맵 차트:
    1. 구성요소가 복잡한 질적 척도를 표현할 땐, 트리맵 차트를 이용하면 보다 효과적이다.
    2. 하나의 큰 사각형을 구성 요소의 비율에 따라 작은 사각형으로 쪼개어 분포를 표현한다.
    3. 사각형 안에 더 작은 사각형을 포함시켜 위계구조를 표현할 수 있다는 것이 장점! 한정된 공간 안에서 많은 구성 요소들의 분포를 체계적으로 표현할 수 있음 'img15'
  • 와플 차트:
    1. 트리맵 차트와 유사하지만 트리맵 차트처럼 위계구조를 표현하진 못함. 'img16'

6. 관계 시각화

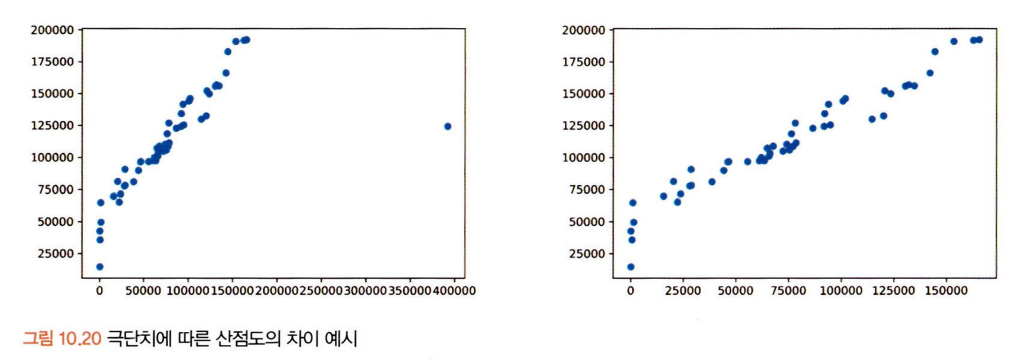
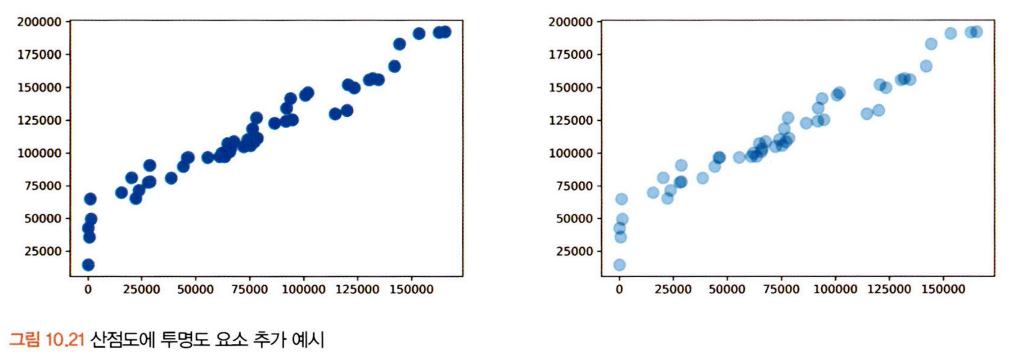
산점도를 그릴 땐 극단치를 제거하고 그리는 것이 좋다. 극단치로 인해 주요 분포 구간이 압축되어 시각화의 효율이 떨어지기 때문. 'img17'

또한 많은 데이터로 인해 점들이 서로 겹친다면, 각 점에 투명도를 주어 밀도를 함께 표현할 수 있다. 'img18'

  • 버블 차트:
    1. 산점도는 2개의 변수 관계만 표현할 수 있지만, 버블 차트는 3요소의 상관관계를 표현 가능.
    2. 버블의 크기를 통해 한 가지 요소를 추가적으로 확인 가능
    3. 버블의 색상, 농도 요소를 추가할 수도 있고 애니메이션 요소를 통해 시간에 따른 변화를 표현할 수 있다.
    4. 원의 면적을 함께 확인해야 하기에, 관측치가 너무 많으면 효율이 떨어짐 -> 관측치가 100개 이상이라면 데이터를 축약하거나 다른 시각화 방법을 사용하는 것이 좋다.

해석할 때, 원의 지름이 아닌 면적을 통해 크기를 판단해야 한다. -> 지름이 2배면 크기는 4배!

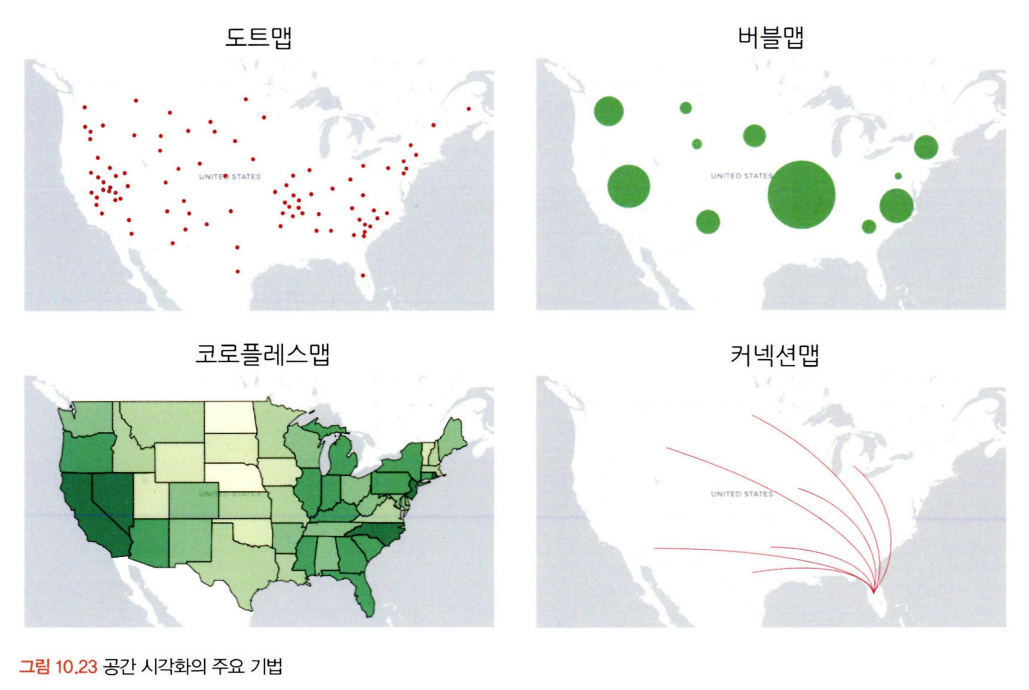
7. 공간 시각화

공간 시각화는 일반적인 시각화 방법처럼 단순 이미지로 표현 X, 지도를 확대하거나 위치를 옮기는 등의 interactive한 활용이 가능하다. 따라서 거시 -> 미시적으로 진행되는 분석 방향과 같이 스토리라인을 잡고 시각화를 적용하는 것이 좋다. 대표적인 방법으로 도트맵, 코로플레스맵, 버블맵, 컨넥션맵 등이 있다.

  • 도트맵:
    1. 지리적 위치에 동일한 크기의 작은 점을 찍어 표현
    2. 시각적으로 데이터의 개요를 파악함에 유리하지만, 정확한 값을 전달하기에 적합하지 않다.
  • 버블맵:
    1. 버블차트를 그대로 지도에 옮겨둔 것.
    2. 비율을 비교하는데 효과적이지만 버블의 영역이 겹칠 수 있기에 이를 잘 조절해야 한다.
  • 코로플레스맵(=단계 구분도)
    1. 데이터 크기에 따라 색상의 음영을 달리하여 해당 지역에 대한 값을 시각화 하는 법
    2. 여러 색상, 투명도, 명도, 채도 등을 혼합하여 표현 가능
    3. 작은 지역들에 비해 큰 지역이 강조되는 인상을 줄 수 있기 때문에 이 점을 유의해야 함
  • 컨넥션맵/링크맵
    1. 지도에 찍힌 점들을 곡선/직선으로 연결하여 지리적 관계를 표현
    2. 연결선의 분포와 집중도를 통해 지리적 관계의 패턴을 파악하기 위해 사용
    3. 지역 간 무역 관계 혹은 항공 경로나 통신 정보 흐름 등을 표현할 때 사용

'img19'

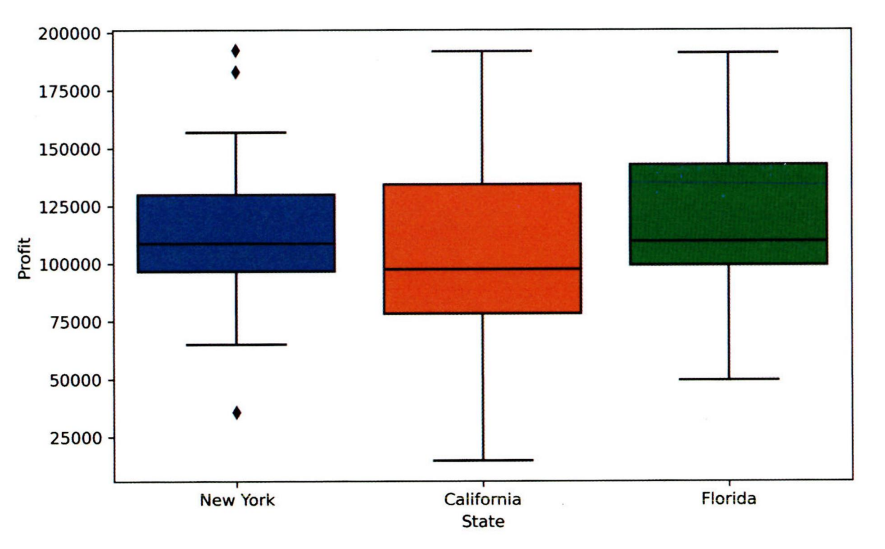
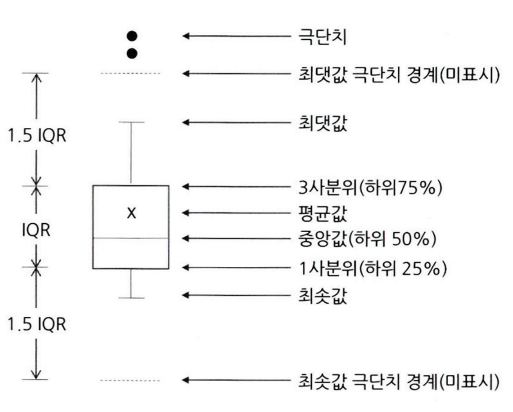
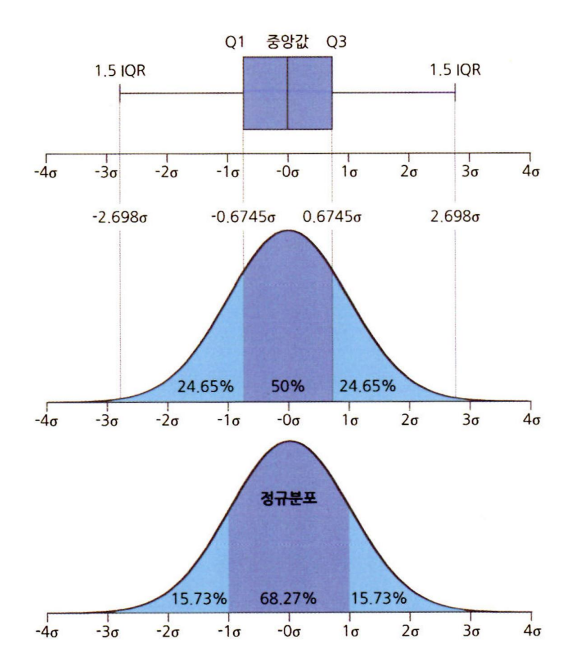
8. 박스 플롯

상자 수염 그림으로도 불리는 박스 플롯. 상자 모양에 최댓값과 최솟값을 나타내는 선이 결합된 모양의 데이터 시각화 방법. 하나의 그림으로 양적 척도 데이터의 분포 및 편향성, 평균과 중앙값 등 다양한 수치를 보기 쉽게 정리해줌. 특히 두 변수의 값이나 카테고리별 분포를 비교할 때 효과적이다.

'img20'

  • 최솟값, 최댓값
  • 제1사분위(25%), 제2사분위(50%), 제3사분위(75%)
  • 최솟값과 최댓값의 범위를 넘어가는 이상치들은 작은 원으로 표기

'img21'

위의 사진에서 중앙값이 다소 아래에 있어 오른쪽으로 치우치고, 오른쪽 꼬리가 긴 분포를 가지고 있음을 유추할 수 있다.

박스 플롯은 데이터의 분포를 정형화시켜 정보를 축약한 것. 두 변수의 박스 플롯을 나란히 놓고 비교하면 각 변수 분포의 차이를 효과적으로 비교할 수 있다. 박스 플롯을 해석할 땐 항상 데이터 분포도를 함께 떠올리는 습관이 필요하다!!

'img22'

KHUDA ML
This post is licensed under CC BY 4.0 by the author.